Model performance

Model Fit, Bias and Variance

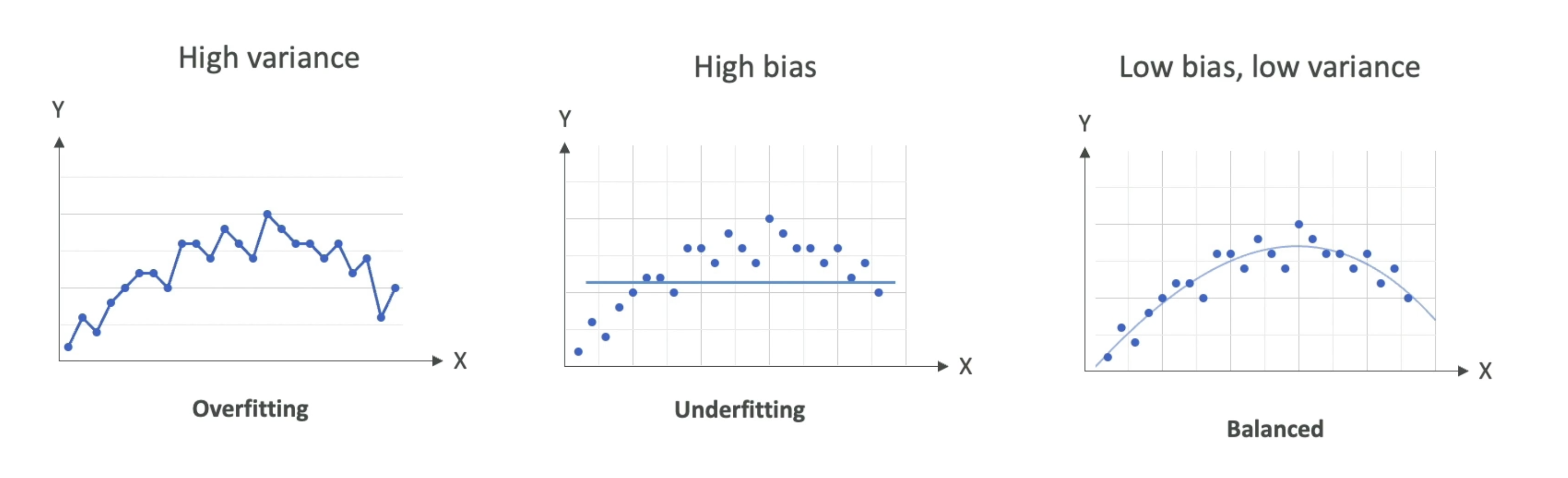
• Model Fit
• Overfitting: models performs well on the training data, but not on the evaluation data
  • Reasons: training data size too small, model trained for too long on a single sample set of data, model complexity is too high (learns from noise)
• Underfitting: model performs poorly on the training data

• Balanced: neither overfitting or underfitting

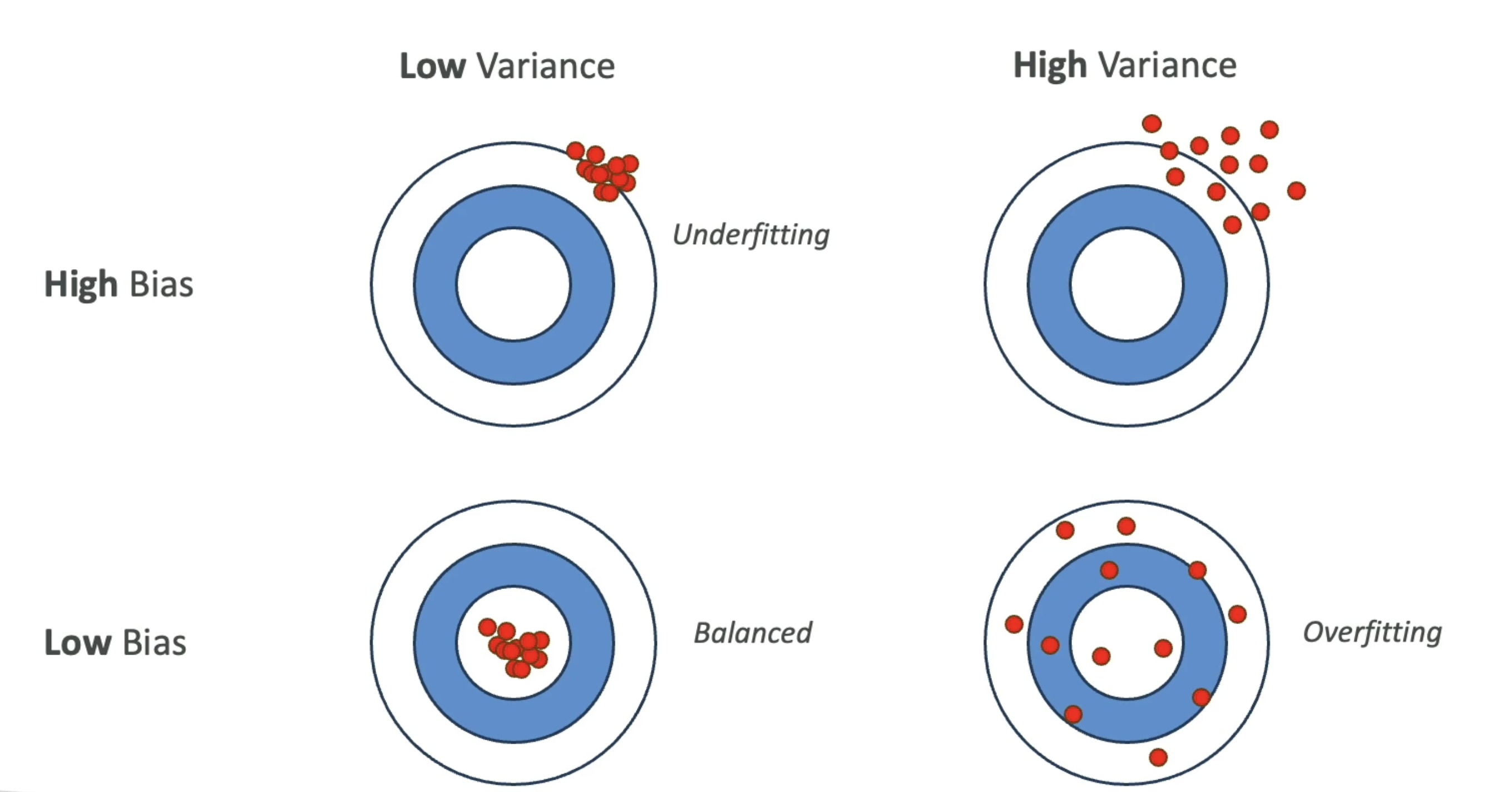
• Bias

• Difference between predicted and actual value
• High bias is bad! E.g., linear regression for a non-linear dataset

• Reduce bias by increasing the number of features

• Variance

• How much the performance of the model changes if trained on a different dataset which has a similar distribution
• Reduce variance by feature selection (less, more important features)

Model Evaluation Metrics

Binary Classification

• E.g., spam/not spam
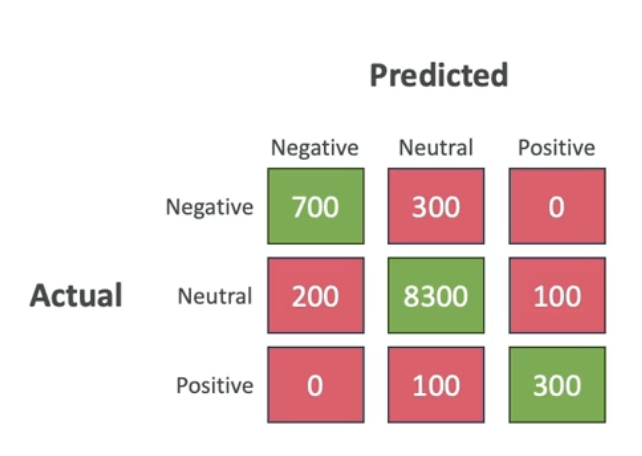
• It's evaluated with a confusion matrix
• True positives (TP), True negatives (TN), False positives (FP), False negatives (FN)
• In an imbalanced dataset FP and FN have different weights (e.g., a FN spam is much worse than FP spam)

$$Precision = \frac{TP}{TP+FP}$$

$$Recall = \frac{TP}{TP+FN}$$

$$F1 = \frac{T2PrecisionRecall}{Precision+Recall}$$

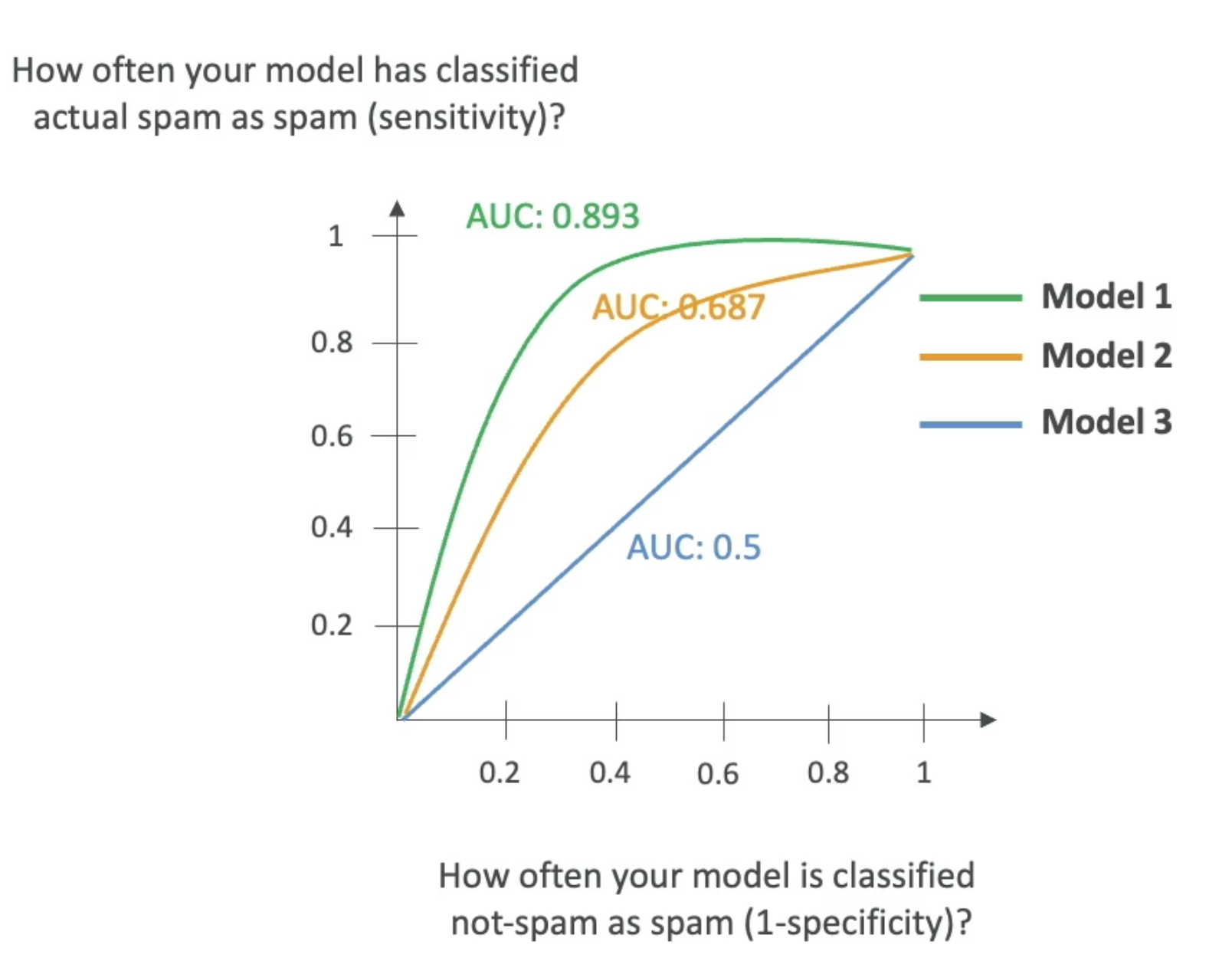
AUC-ROC

• Area Under Curve - Receiver Operator Curve
• Value from 0 to 1 (1 is perfect model)
• Uses sensitivity (TP rate) and I-specificity (FP rate)
• AUC-ROC shows what the curve for TP compared to FP looks like at various thresholds

Regression Metrics

These are metrics used for evaluating models that predict a continuous value

• MAE: Mean Absolute Error
• Between predicted and actual values

$$MAE = \frac{1}{n} \displaystyle \sum_{i=1}^n |y_i - \overline{y_i}|$$

• MAPE: Mean Absolute Percentage Error

$$MAPE = \frac{1}{n} \displaystyle \sum_{i=1}^n |\frac{y_i - \overline{y_i}}{\overline{y_i}}|$$

• RMSE: Root mean squared error

$$RMSE = \sqrt{\displaystyle \sum_{i=1}^n \frac{(\overline{y_i} - y_i)^2}{n}}$$

• R Squared
• Explains variance in your model
• $Rˆ2$ close to 1 means predictions are good